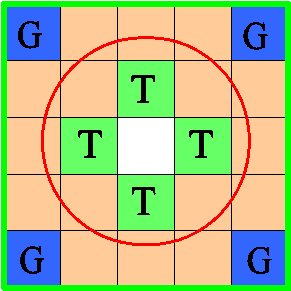
In a square box 5x5 there are 24 bars 1x1 (the place of one bar is free). On four bars the guards are drawn, on the other four bars the tigers are drawn, on sixteen bars pieces of a lattice are drawn.
In an initial position the tigers are in a trap, the guards are outside of a trap (there is an empty place it the centre of a box). Moving bars to the center of a box, it is possible to let out tigers, and to hide guards in a trap. How can you do it? How many bar moves least is required for this?
Do you think it is possible to give back one guard to tigers?
In an initial position the tigers are in a trap, the guards are outside of a trap (there is an empty place it the centre of a box). Moving bars to the center of a box, it is possible to let out tigers, and to hide guards in a trap. How can you do it? How many bar moves least is required for this?
Do you think it is possible to give back one guard to tigers?
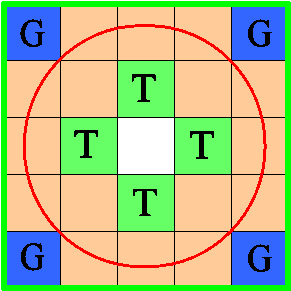
The sizes of a trap are slightly increased as shown in drawing. The presence of "empty" bars allows to alter a puzzle: all of them (or two diagonal) are rigidly fixed.
Solve the tasks in both cases: all the bars move freely and "empty" bars (or their part) are fixed.
Solve the tasks in both cases: all the bars move freely and "empty" bars (or their part) are fixed.
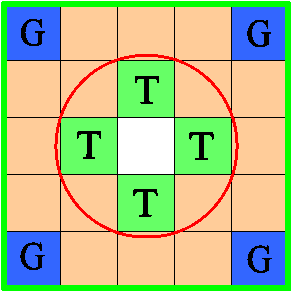
You can reduce the sizes of a trap: there are the pieces of a lattice only on eight bars. As a result you will have another, simpler puzzle.
How are the previous tasks for this case solved?
How are the previous tasks for this case solved?